Тиханова Лариса Александровна
учитель математики
МБОУ «Киятская СОШ Буинского муниципального района РТ»
с.Кият
Цели: 1. Закрепить ранее полученные знания, умения и навыки по теме.
2. Развивать внимание учащихся и их математическую речь.
3. Воспитывать сознательное отношение к учебе.
Задачи:
1.Закрепить формирование навыков сознательного выбора решения уравнений и
неравенств; осознать место темы в ГИА, ее значимость.
2.Развивать потребность в нахождении рациональных способов решения;
3.Воспитывать умение контролировать внимание на всех этапах урока.
Тип урока: урок обобщения и систематизации теоретических и практических
знаний, умений и навыков
I Учитель: (психологическая установка учащимся) Говорят, что человек, не знающий математики, подобен путнику, блуждающему в лабиринте… А человек, вооруженный математическими знаниями, подобен птице, парящей над этим лабиринтом. Посмотрите на эпиграф к нашему занятию и попробуйте сформулировать: чем мы сегодня будем заниматься? Я предлагаю вам ответить на вопросы: Кто ты? Путник или птица? Как ты?
Плутаешь или паришь?
Сухие строки уравнений –
В них сила разума влилась.
В них объяснение явлений,
Вещей разгаданная связь.
Л.М. Фридман
Сегодня у нас повторительно-обобщающий урок по теме «Уравнения и неравенства с одной переменной»
II Итак, на доске записаны уравнения:
1.4x2 + 11x = 3
2.18y3 – 36y = 0
3.2x + 7 = 2x – 3
4.x4 – 13x2 + 36 = 0
5.(x2 + 2x)( x2 + 2x –2) = 3
6.(3x – 1)2 = 5x – 10
7.x6 – x4 + 5x2 – 5 = 0
8.7x + 2 = 0
9.2x2 – 10 = 0
Вопросы:
Какие уравнения линейные или преобразуются в линейные?
Может ли в линейном уравнении быть ответ «корней нет»? Привести пример?
Решить устно уравнение номер 8
Решить устно уравнение номер 3
При каком условии квадратное уравнение не имеет корней? Два корня? Один?
Какие способы решений уравнения знаем, кроме линейных и квадратных?
Какие уравнения можно решить способом разложения на множители?
Какое разложение применяем в уравнении под номером 2?
Какое разложение применяем в уравнении под номером 7?
Какие из этих уравнений можно решить способом замены переменной?
Какую замену сделаем в уравнении под номером 4, под номером 5?
III Решаем уравнения под номером 2, 7, 4 и 5
2. 18y3 – 36y = 0
Ответ: y = 0; √2; – √2.
7. x6 – x4 + 5x2 – 5 = 0
Ответ: x = 1; -1.
4. x4 – 13x2 + 36 = 0
Ответ: x = 3; -3; 2; -2.
Подвели итоги.
IV Переходим к работе над неравенствами.
– Умеем решать квадратное неравенство, используя схему параболы
– Повторим различные случаи записи ответов
На доске даны схемы:
1. 2. 3.
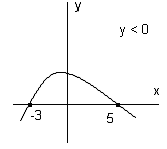
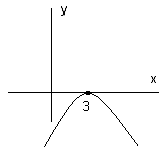
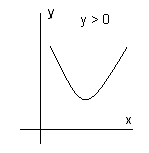
4. 5.
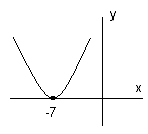
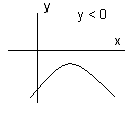
– Записать ответ в каждом случае
– Какой еще способ решения неравенства мы изучили?
– Некоторые квадратные неравенства можно решать разными способами
– Решить неравенство 0,25 – x2 > 0 двумя способами (на закрытой доске решают двое учеников, остальные в тетради)
1) 0,25 – x2 = 0 2) (0,5 – x)(0,5 + x) > 0
x1 = 0,5 x2 = -0,5
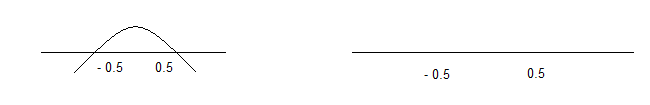
Ответ: (-0,5; 0,5).
На доске открывается решение для проверки.
V. На доске даны задания.
1. Решить неравенство
2x2 + 5x – 7 < 0
2. Решить неравенство
x2 + x − 12 ≤ 0
3. Решить неравенство
![]()
4. При каких значениях x выражение имеет смысл?
![]()
5. При каких значениях a уравнение не имеет корней?
a x2 + x + 3 = 0
6. При каких значениях a уравнение имеет два корня?
2 x2 + ax + a – 2 = 0
Кто сколько сделал заданий? Отметить.
VI. Применение уравнений в решении математических, геометрических, физических, химических задач.
«Уравнения и неравенства используются во многих науках: геометрии, химии, физике»
Геометрия
Определить число сторон правильного многоугольника;
Вычислить сторону ромба, если его диагонали 4,6 см и 6,4 см;
Физика
Вагон массой 20 т, движущийся со скоростью 0,3 м/с, догоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после взаимодействия, если удар неупругий?
Химия
Какой объем оксида серы при нормальных условиях получится при сгорании одного килограмма серы?
Неравенства в математике и в физике
Если туристы будут проходить в день на 5 км меньше, то они пройдут за 8 дней расстояние, меньшее 90 км. Если же они будут проходить в день на 5 км больше, то за 6 дней они пройдут расстояние, большее 90 км. Сколько километров в день проходят туристы?
VII. Итог урока. Рефлексия.
-Вернемся к вопросу, заданному в начале урока: Кто ты? Путник или птица? Как ты? Плутаешь или паришь?
-Спасибо за урок. Вы отлично поработали!
VIII. Домашнее задание: продумать план реализации проекта «Нам уравнения строить и жить помогают»






