
Кунгурова Гульназ Рафаэловна
учитель математики
МБОУ «СОШ №26»
г. Нижнекамск, Республика Татарстан
Пояснительная записка
Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. В школе уравнениям и неравенствам, содержащим переменную под знаком модуля, уделяется достаточно мало внимания. Необходимость рассмотрения данной темы обусловлена тем, что задания содержащие модуль вызывают у учащихся значительные проблемы. Задания подобного типа регулярно встречаются в материалах ЕГЭ как в базовой части, так и в заданиях повышенного и высокого уровня сложности. Вместе с тем, решение уравнений, содержащих переменную под знаком модуля, является эффективным способом повторения и закрепления навыков решения других видов уравнений и способов их решения: линейных, квадратных, дробно-рациональных, тригонометрических, показательных, логарифмических. А также, закрепляется умение решать различные виды неравенств, систем и совокупностей. Понятие модуля (абсолютной величины) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел. Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Однако программой школьного курса не предусмотрены обобщение и систематизация знаний о решении заданий с модулем. Считаю, что тема представлена недостаточно для того, чтобы даже наиболее подготовленные обучающиеся уверенно могли выполнять задания второй части на ЕГЭ по математике. Задание с модулем в ЕГЭ может встретиться в 9 задании ( преобразование выражений) , в 15 задании ( неравенства) , или в 18 (задание с параметром), или вообще явно модуля не будет, но в процессе решения потребуются знания данного понятия.
Данная программа является развитием ранее приобретенных программных знаний. Она дополняет базовую программу, не разрушая ее целостности, расширяет и углубляет знания учащихся и реализует принцип преемственности между средней школой и высшим образованием.
Главной целью программы является изучение различных методов решения уравнений и неравенств , построения графиков функций, содержащих переменную под знаком модуля.
Задачи программы:
– привлечь внимание учеников к этим задачам, привлечь их интерес к их решению, выработать и закрепить прочные навыки решения задач, в которых переменная находится под знаком модуля; -проработать определение и некоторые свойства модуля; -изучить теоретический материал по решению уравнений и неравенств, содержащих переменную под знаком модуля; -освоить решение простейших уравнений и неравенств с модулем через равносильные переходы -рассмотреть различные методы решения уравнений и неравенств с модулем.
Структура программы представляет собой три логически законченные и содержательно взаимосвязанные темы , изучение которых обеспечит системность и практическую направленность знаний и умений учеников. Разнообразный дидактический материал дает возможность отбирать дополнительные задания для учащихся различной степени подготовки. Все занятия направлены на расширение и углубление базового курса. Содержание программы можно варьировать с учетом склонностей, интересов и уровня подготовленности учеников.
Основной тип занятий – практикум. Для наиболее успешного усвоения материала планируются различные формы работы с учащимися: лекционные и практические занятия, с использованием презентаций, групповые, индивидуальные формы работы. Для текущего контроля учащимся рекомендуется серия заданий, часть которых выполняется в классе, а часть – дома самостоятельно. Изучение данного курса заканчивается проведением контрольной работы.
Актуализация темы
Задания, содержащие переменную под знаком модуля очень часто вызывают у учащихся наибольшие затруднения., потому что они являются непривычными, сложными. Эти задания представляют сложность в логическом, техническом и психологическом плане. Именно такие задания играют важную роль в формировании логического мышления и математической культуры учащихся , и они являются материалом для настоящей учебно-исследовательской работы
Содержание программы ( 17 часов)
1. Введение( 2 часа)
Понятие о модулях. Контрольные значения подмодульного выражения. Постановка задач, содержащих выражения подл знаком модуля. Понятие об основных методах решения задач с модулем.
Основная цель– сформировать у обучающихся понятие о модуле, познакомить учащихся с многообразием вопросов в задачах с модулем, с основными методами их решений- аналитическим и использованием графических интерпретаций
2. Аналитические методы решения задач, содержащих выражения с переменной под знаком модуля ( 10 часов)
Линейные уравнения, неравенства , системы линейных уравнений, содержащие выражения с переменной под знаком модуля. Квадратные уравнения и неравенства, содержащие выражения с переменной под знаком модуля. Рациональные и иррациональные уравнения и неравенства, , содержащие выражения с переменной под знаком модуля.
Основная цель- систематизировать умения обучающихся в решении рациональных и иррациональных уравнений и неравенств; сформировать умения решать уравнения и неравенства у казанных видов , при наличии переменной под модулем. Изучение темы начинается с элемента повторения курса основной щколы – решения линейных, квадратных, дробны уравнений и неравенств, иррациональных уравнений. Решению дробных уравнений ≠предшествует введение понятия равносильности. Его появление требует глубокой отработки: основное внимание следует уделить процессу осмысления выполнения преобразований в ходе решения уравнений и неравенств, приводящих к равносильным уравнениям и неравенствам, системам.
В процессе обучения решению уравнений и неравенств с модулем акцент делается на разбиение контрольными значениями множества значений подмодульного выражения на подмножества, и решения исходной задачи на каждом из образовавшихся подмножеств, в контрольных значениях
3. Функции и их графики ( 5 часов)
Свойства функций у=, у= и их графики. Построение графиков функций у=f(х-a)+b, у=аf(bх). Построение графиков функций и уравнений, выражения которых содержат знак модуля.
Основная цель- Систематизировать знания обучающихся о функциях у=( p € R, p), у=, (n € N, n>2) , систематизировать умения построения графиков функций с использованием параллельного переноса, растяжения и сжатия и симметрии.
Основное внимание уделяется отработке навыков: построения областей, заданных неравенствами, системами неравенств; выполнения необходимых преобразований, направленных на приведение уравнений или неравенств к виду, удобному для изображения линий или областей, заданных уравнениями или неравенствами соответственно.
Простейшие уравнения и неравенства с модулем
К простейшим уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов:
Примеры решения простейших уравнений.
Пример 1. Решим уравнение .
Решение.
Ответ. .
Пример 2. Решим уравнение .
Решение. Ответ. .
Пример 3. Решим уравнение . Решение. Ответ. .
Ряд уравнений решается с использованием следующей теоремы.
Теорема.4 Сумма модулей равна алгебраической сумме подмодульных величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму.
Пример 5. Решить уравнение
Решение. Так как , то мы имеем равенство вида , где , . Поэтому исходное уравнение равносильно системе:
Ответ. .
Примеры решения простейших неравенств.
Пример 6. Решим неравенство .
Решение. . Ответ. .
Пример 7. Решим неравенство .
Решение.
Ответ. .
Как ни странно, но достаточно, чтобы избавиться от знака модуля в любых неравенствах.
Пример 8 . Решить неравенство
Решение.
Ответ. .
Графическое решение уравнений и неравенств с модулем
Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры).
Пример 9 . Для каждого значения a укажите число решений уравнения
Решение. Построим график функции . Для этого выделим полный квадрат : Число точек пересечения графика функции у = с горизонтальными прямыми у = а равно числу решений уравнения.
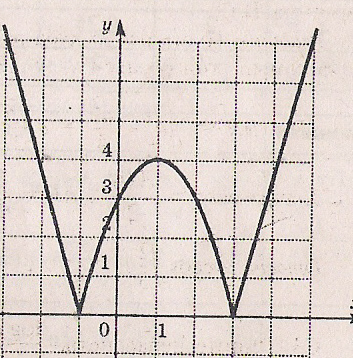 Ответ: если < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
Ответ: если < 0, то решений нет; если а= 0, то два решения, если 0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
Способы решения уравнений и неравенств с модулем.
Метод раскрытия модулей.
Пример 10. Решить уравнение
Решение. Это уравнение содержит более одного модуля.
Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем.
1. Найти значения переменной, при которых каждый из модулей обращается в нуль: , ; , ; , .
2. Отметить эти точки на числовой прямой.
3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями.
1) При или . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях из этого промежутка выражение будет положительным.
Возьмем значение из промежутка и подставим его значение в выражение , получаем , значит на этом промежутке отрицательно, а следовательно “выйдет” из под модуля со знаком “минус”, получим: .
При этом значении , выражение получит значение , значит, оно на промежутке также принимает отрицательные значения и “выйдет” из модуля со знаком “минус”, получим: .
Выражение получит значение и «выйдет» из под модуля со знаком “минус”: .
Уравнение на этом промежутке получится таким: , решая его, находим: .
Выясняем, входит ли это значение в промежуток . Оказывается входит, значит является корнем уравнения.
2) При . Выбираем любое значение из этого промежутка. Пусть . Определяем знак каждого из выражений под модулем при этом значении . Оказывается, что выражение положительно, а два других отрицательны.
Уравнение на этом промежутке примет вид: . Решая его, находим . Это значение не входит в промежуток , а значит, не является корнем уравнения.
3) При . Выбираем произвольное значение из этого промежутка, скажем, и подставляем в каждое из выражений. Находим, что выражения и положительны, а – отрицательно. Получим следующее уравнение: .
После преобразования, получим: , а значит, уравнение не имеет корней на этом промежутке.
4) При . Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: , , которое входит в промежуток и является корнем уравнения.
Решение уравнений, содержащих модули неотрицательных выражений
Пример 11. Чему равна сумма корней уравнения (корень, если он один) уравнения
Решение. Рассмотрим выражение
и преобразуем его к виду
Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если (т.к. ). Преобразуем полученное выражение, при условии . Получим уравнение, равносильное исходному:
Ответ. .
Пример 12. Решить уравнение Решение. Поскольку левая часть уравнения неотрицательна, при всех допустимых значениях переменной, на множестве корней уравнения правая его часть тоже должна быть неотрицательной, отсюда условие , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение . Решая его и учитывая ограничение , получаем
Решение уравнений с использованием геометрической интерпретации
Геометрический смысл выражения – длина отрезка координатной оси, соединяющего точки с абсциссами и . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
Пример 13. Решим уравнение .
Решение. Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка обладают требуемым свойством, а точки, расположенные вне этого отрезка, – нет.
Ответ.
Пример 14 . Решить неравенство .
Решение. Изобразим на координатной прямой точки, сумма расстояний от которых до точек и в точности равна . Это все точки отрезка . Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
Ответ. .
Решение уравнений с использованием тождества
Пример 15. Решить уравнение
Решение. Дважды применяя тождество , получим уравнение
решением которого является интервал .
Ответ. .
Пример 16. Решить уравнение
Решение. .
Ответ. .
Применение теоремы о знаках при решении уравнений
Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей:
Теорема . Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений.
Пример 17. Решить неравенство
Решение. Воспользуемся теоремой:
Используя формулу разности квадратов, разложим числитель и знаменатель на множители и решим полученное рациональное неравенство.
Ответ.
Решение уравнений переходом к следствию
Все уравнения с модулями могут быть решены следующим образом: рассмотрим весь набор уравнений, который может получится при раскрытии модулей, но не будем выписывать соответствующие промежутки. Решая каждое из полученных уравнений, получим следствия исходного уравнения. Остается только проверить не приобрели ли мы посторонних корней прямой их подстановкой в исходное уравнение.
Пример 18. Решим уравнение
Решение. Последовательно переходя к следствиям, получаем:
Нетрудно убедиться, что найденные числа не являются корнями исходного уравнения.
Ответ. нет решения.
Решение неравенств методом интервалов
Применение метода интервалов основано на следующей теореме.
Теорема . Функция, непрерывная на промежутке и необращающаяся на нем в нуль, сохраняет на этом промежутке свой знак.
Это означает, что нули функции и границы промежутков ее непрерывности разделяют область определения функции на участки, где она сохраняет постоянный знак. Применение метода поясним на примере.
Пример 19. Решим неравенство
Решение. Пусть . Областью определения данной функции есть . Решая уравнение получим, что функция не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения.
Ответ. .
Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток).
Решение уравнений домножением на положительный множитель
Пример 20. Решить неравенство
Решение. Ловушка” заключается в том, что в задаче имеется несколько модулей, раскрывать которые – значит получить, громоздкое решение. Умножим дробь на некоторое выражение, принимающее лишь положительные значения и такое, чтобы упростить исходное неравенство:
Ответ. .
Тест №1
Первый уровень сложности
1. Найти сумму корней уравнения 25+25 х+6=0
а) 2,5
б) -1
в) 13
г) 4
2. Решить неравенство и найти наибольшее целое решение 3- 10х – 8 ≥ 0
а) 13
б) 3
в0-5
г) 0
3. Решить уравнение =2х-1
а)3
б)0;3
в)2; -5
г)нет корней
4. Решить неравенство < 5
а) ( 0;
б) (2;4)
в) 0;]
г)-3;0)
5. Решить систему неравенств
а)(-7;-4] б) -4;4]
в)(-6;0)
г) нет решений
6. Составить квадратное уравнение, если его корни равны 2 и -5
а) +3х-10=0
б)-3х +10=0
в) -7х+2=0
г)+2х-5=0
Тест №2
Второй уровень сложности
1. Решить уравнение и найти сумму корней – =55
а)-2
б)14
в)7
г)10
2. Найти наибольшее целое решение неравенства -3+7х +6 > 0
а) 2
б)3
в)4
г)5
3.Решить уравнение =
а) 3
б) -4
в) нет корней
г)2
4. Решить неравенство
а)( –
б) (-2;3)
в)]
г)
5. Решить систему неравенств и найти сумму его целых решений
а) -18
б)-17
в)13
г)2
6. Решить уравнение =5-3х
а) 1
б)
в)
г) 2
Тест №3
1. Решить уравнение и найти сумму корней + = +
а)15
б)-12
в)10
г)нет корней
2. Решить неравенство +4х +4≥ 0
а) 4
б)любое число
в)-3
г) нет решения
3. Решить уравнение 1+
а)-7;7
б)-3;7
в)-3;3
г)1;5
4. Решить неравенство >9
а)(8;+
б)(-
в)(4;7)
г)(-
5. Пусть (х;у) решение системы уравнений. Найти сумму х+у
а)2
б)-3
в)-2
г)5
6. Решить уравнение =
а)2
б)10
в)-4
г)11
Контрольная работа №1
Первый уровень сложности
1. Решите уравнение ( ) =х(
2. Решите неравенство > 0
3. Решите уравнение = х+7
4. Решить неравенство ≥ х-6
5. Решить неравенство ≥ 7х+29
Контрольная работа №1
Второй уровень сложности
1. Решить уравнение + =3
2. Найти сумму целых решений неравенства + ≥1
3 Решить уравнение
4. Решить неравенство
5. Решить неравенство
Контрольная работа №2
Первый уровень сложности
1. Решить графически систему уравнений
2. Построить графики функций у=у= (, ,
если f(х)=4-2х
3. Построить график функции у=-3+2
Контрольная работа №2
Второй уровень сложности
1. Решить графически систему уравнений
2. Построить графики функций у=у=(, ,
если f(х) = 5 .
3. Построить график функции у=1
Список литературы:
1. Мордкович, А. Г. Алгебра и начала математического анализа. 11 класс: в 2 ч. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. – 4-е изд., стереотип. – М.: Мнемозина, 2018. – 287 с.
2. Вавилов, В. В. Задачи по математике. Уравнения и неравенства: справочное пособие / В. В. Вавилов, И. И. Мельников, С. Н. Олехник, П. И. Пасиченко. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 240 с.
3. Горнштейн, П. И. Экзамен по математике и его подводные рифы / П. И. Горнштейн, А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – М.: Илекса, Харьков: Гимназия, 1998. – 236 с.
4 . ЕГЭ. Математика. Профильный уровень. Высший балл / сост. Т. М. Ерина. – М.: Экзамен, 2017. – 350 с. (Серия «ЕГЭ. Высший балл»)
5. Зеленский, А. С. Решение уравнений и неравенств с модулем / А. С. Зеленский, И. И. Панфилов. – М.: Научно-технический центр «Университетский»: УНИВЕР-ПРЕСС, 2009. – 112 с. (Серия «Математика: перезагрузка»)
6. Колесникова, С. И. «Поиграем» с равносильными переходами в уравнениях и неравенствах с модулями / С. И. Колесникова // Потенциал. Математика, физика, информатика. – 2010. – №08 (68). – С. 22-30.
7. Математика: Модуль №2 для 10 класса. Учебно-методическая часть / сост. Т. А. Осетрова. – Красноярск: Красноярский гос. ун-т, 2006. – 41 с. 102
8. Мерзляк, А. Г. Алгебраический тренажер: пособие для школьников и абитуриентов / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – М.: Илекса, 2007. – 320 с.
9. Шарыгин, И. Ф. Факультативный курс по математике: Решение задач: учеб. пособие для 10 класса средней школы. – М.: Просвещение, 1989. – 252 с.
10. Яковлев, И. В. Уравнения с модулем [Электронный ресурс] / И. В. Яковлев // Материалы по математике. MathUs.ru [Электронный ресурс]. – Режим доступа: https://docplayer.ru/27596288-I-v-yakovlev-materialy-pomatematike-mathus-ru-uravneniya-s-modulem.html
11. Яковлев, И. В. Уравнения и неравенства с модулем [Электронный ресурс] / И. В. Яковлев, А. Г. Малкова // Материалы по математике. MathUs.ru. – Режим доступа: https://docplayer.ru/27596962-Uravneniya-ineravenstva-s-modulem.html

