Портнова Светлана Борисовна
учитель-дефектолог
ГБОУ «Казанская школа-интернат № 1»
г. Казань, Республика Татарстан
Особого внимания требует методика обучения математике в классах
коррекционно-развивающего обучения VII вида, а так же в классах с детьми
ОВЗ, так как обучение математике в этих классах имеет свою специфику. У
учащихся с задержкой психического развития, при изучении предмета
возникают серьезные проблемы, связанные с тем, что объем знаний по
математике минимален, приемы общеурочной деятельности не
сформированы, ослаблены память и внимание, мыслительные процессы
протекают медленно. Содержание учебного материала, темп обучения,
требования к результатам обучения, как правило, оказываются для детей с
ОВЗ непосильными. Это не позволяет им активно включаться в учебный
процесс, а также формируют у них негативное отношение к учебе. Поэтому
обучение математике должно осуществляться на доступном уровне для такой
категории школьников. Для эффективного обучения детей с ограниченными
возможностями здоровья важно формировать у них познавательный интерес,
желание и привычку думать, стремление узнать что-то новое.
Цели обучения математике для детей с ОВЗ следующие:
• овладение комплексом минимальных математических знаний и
умений, необходимых для повседневной жизни, будущей
профессиональной деятельности (которая не требует знаний
математики, выходящих за пределы базового курса), продолжения
обучения в классах общеобразовательных школ;
• развитие логического мышления, пространственного воображения и
Особого внимания требует методика обучения математике в классах
коррекционно-развивающего обучения VII вида, а так же в классах с детьми
ОВЗ, так как обучение математике в этих классах имеет свою специфику. У
учащихся с задержкой психического развития, при изучении предмета
возникают серьезные проблемы, связанные с тем, что объем знаний по
математике минимален, приемы общеурочной деятельности не
сформированы, ослаблены память и внимание, мыслительные процессы
протекают медленно. Содержание учебного материала, темп обучения,
требования к результатам обучения, как правило, оказываются для детей с
ОВЗ непосильными. Это не позволяет им активно включаться в учебный
процесс, а также формируют у них негативное отношение к учебе. Поэтому
обучение математике должно осуществляться на доступном уровне для такой
категории школьников. Для эффективного обучения детей с ограниченными
возможностями здоровья важно формировать у них познавательный интерес,
желание и привычку думать, стремление узнать что-то новое.
Цели обучения математике для детей с ОВЗ следующие:
• овладение комплексом минимальных математических знаний и
умений, необходимых для повседневной жизни, будущей
профессиональной деятельности (которая не требует знаний
математики, выходящих за пределы базового курса), продолжения
обучения в классах общеобразовательных школ;
• развитие логического мышления, пространственного воображения и
Особого внимания требует методика обучения математике в классах
коррекционно-развивающего обучения VII вида, а так же в классах с детьми
ОВЗ, так как обучение математике в этих классах имеет свою специфику. У
учащихся с задержкой психического развития, при изучении предмета
возникают серьезные проблемы, связанные с тем, что объем знаний по
математике минимален, приемы общеурочной деятельности не
сформированы, ослаблены память и внимание, мыслительные процессы
протекают медленно. Содержание учебного материала, темп обучения,
требования к результатам обучения, как правило, оказываются для детей с
ОВЗ непосильными. Это не позволяет им активно включаться в учебный
процесс, а также формируют у них негативное отношение к учебе. Поэтому
обучение математике должно осуществляться на доступном уровне для такой
категории школьников. Для эффективного обучения детей с ограниченными
возможностями здоровья важно формировать у них познавательный интерес,
желание и привычку думать, стремление узнать что-то новое.
Цели обучения математике для детей с ОВЗ следующие:
• овладение комплексом минимальных математических знаний и
умений, необходимых для повседневной жизни, будущей
профессиональной деятельности (которая не требует знаний
математики, выходящих за пределы базового курса), продолжения
обучения в классах общеобразовательных школ;
• развитие логического мышления, пространственного воображения и
Тема: «Обобщающий урок по геометрии»
Класс: 5
Адаптированная основная образовательная программа образования обучающихся с умственной отсталостью (интеллектуальными нарушениями).
Тип урока: урок комплексного применения знаний и умений (урок закрепления).
Формы проведения урока: фронтальная, индивидуальная.
Цель: Повторить начальные геометрические понятия, обобщить полученные представления о простейших геометрических фигурах.
Задачи:
– Учебные: учить использовать приобретенные знания и умения в практической деятельности и повседневной жизни; закрепление умений и навыков геометрических построений с помощью линейки, циркуля, чертежного угольника; конструирование из различных геометрических фигур
– Развивающие:
активизировать познавательную деятельность учащихся через решение
практических задач, развивать логическое мышление; развивать умения
анализировать и делать выводы.
Воспитательные:
воспитывать у учащихся интерес к предмету, доброжелательность;
воспитывать стремление к совершенствованию знаний.
Оборудование:
Плакат с изображением планет
Таблички с основными геометрическими фигурами
Индивидуальный конверт с различными геометрическими фигурами (раздаточный материал)
Индивидуальные карточки с рисунком планеты (раздаточный материал)
Цветные карандаши
Линейки
Циркули
Иллюстративный материал к стихотворениям
Таблички и карточки с изображенными на них фигурами (самолеты)
Ковер из геометрических фигур (образец)
I. Организация урока.
Ознакомить обучающихся с темой и целями урока.
II. – Сегодня у нас необычный урок. Это урок-путешествие в страну Геометрию. Для того, чтобы совершить путешествие, определим маршрут, по которому мы полетим.
(на доске прикреплен плакат с изображениями планет, которые прикрыты табличками. Чтобы прочитать названия планет, дети должны назвать фигуры, изображенные на табличках).
|
|
|
|
|
|
|
|
|
|
|
|
|
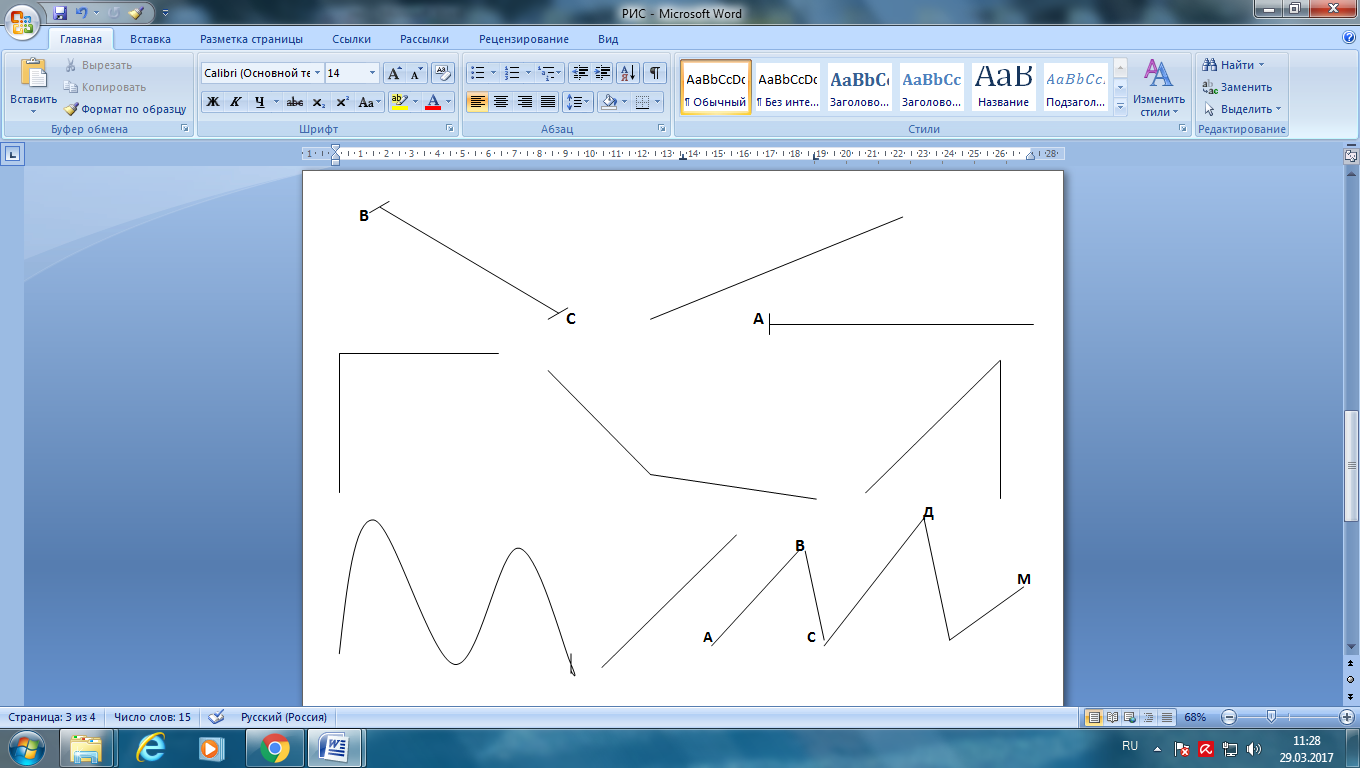
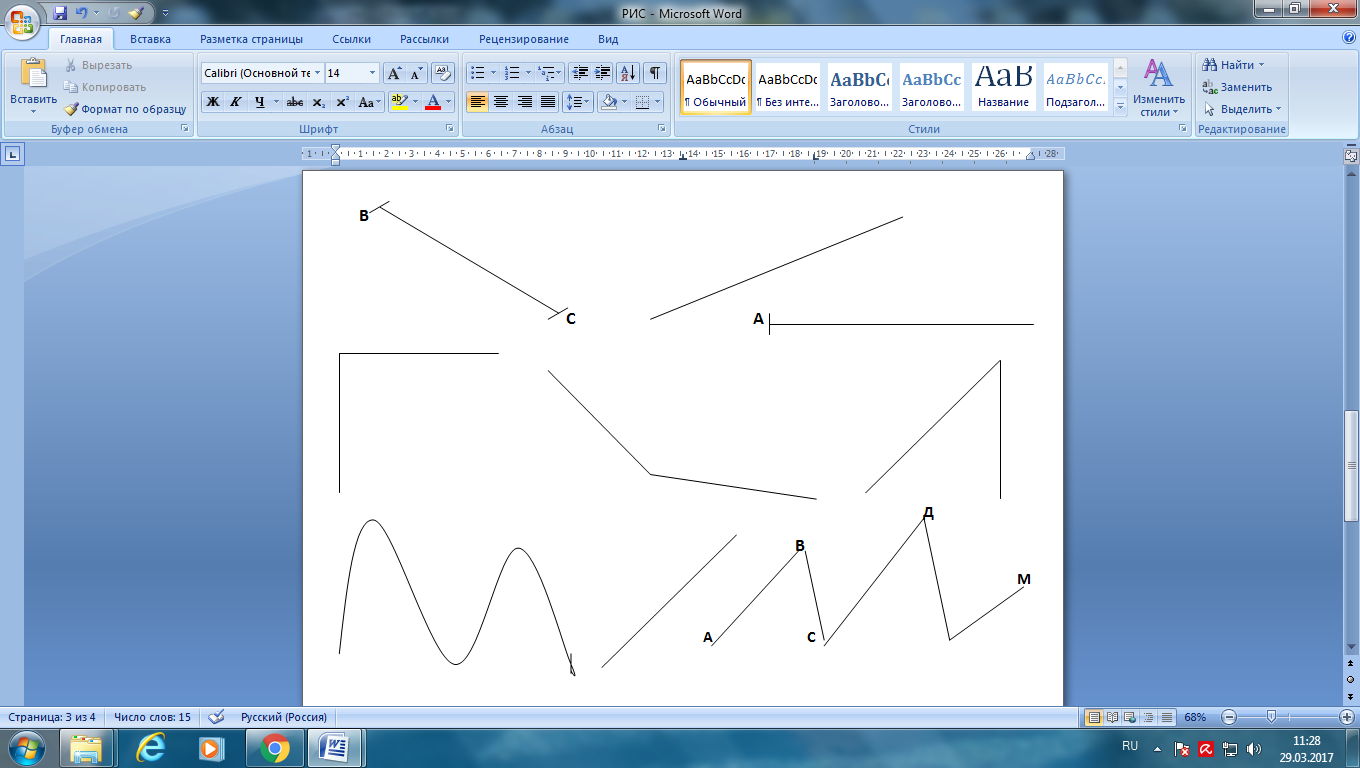
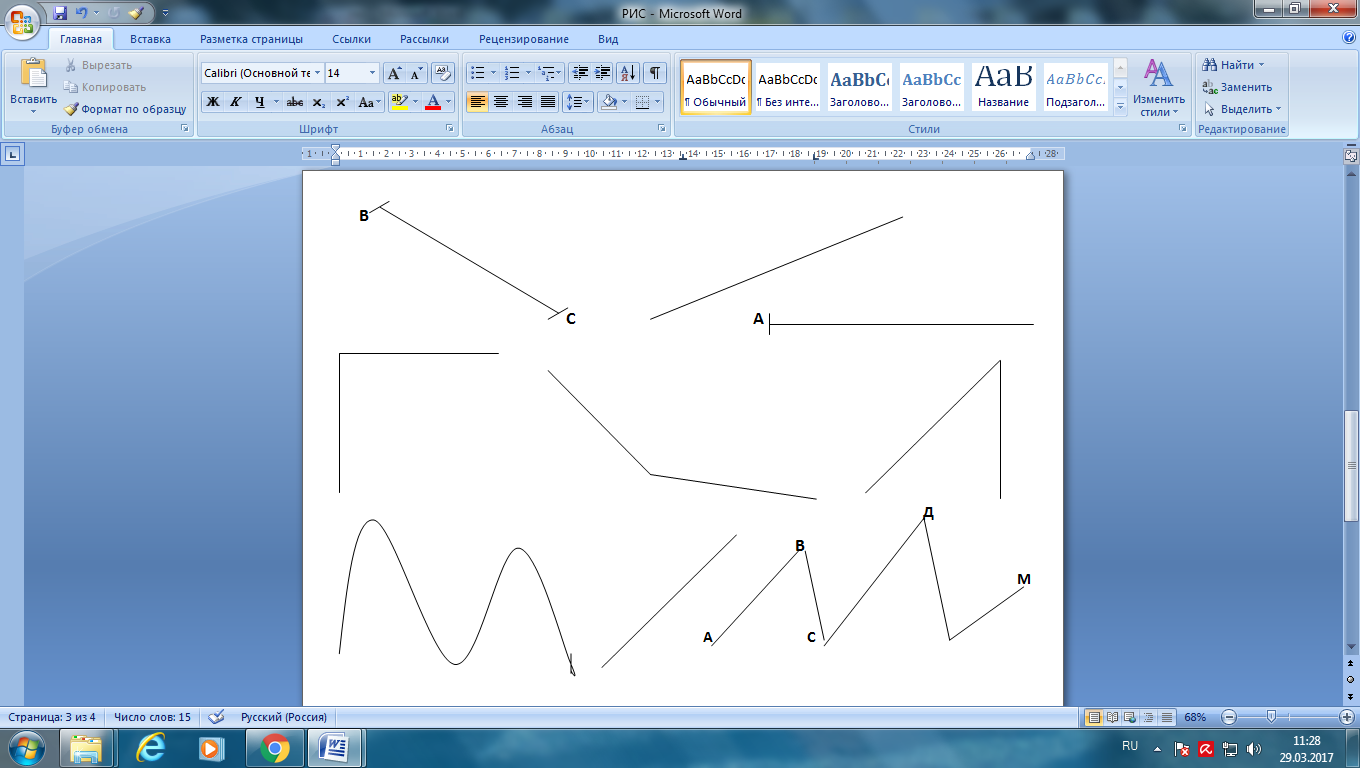
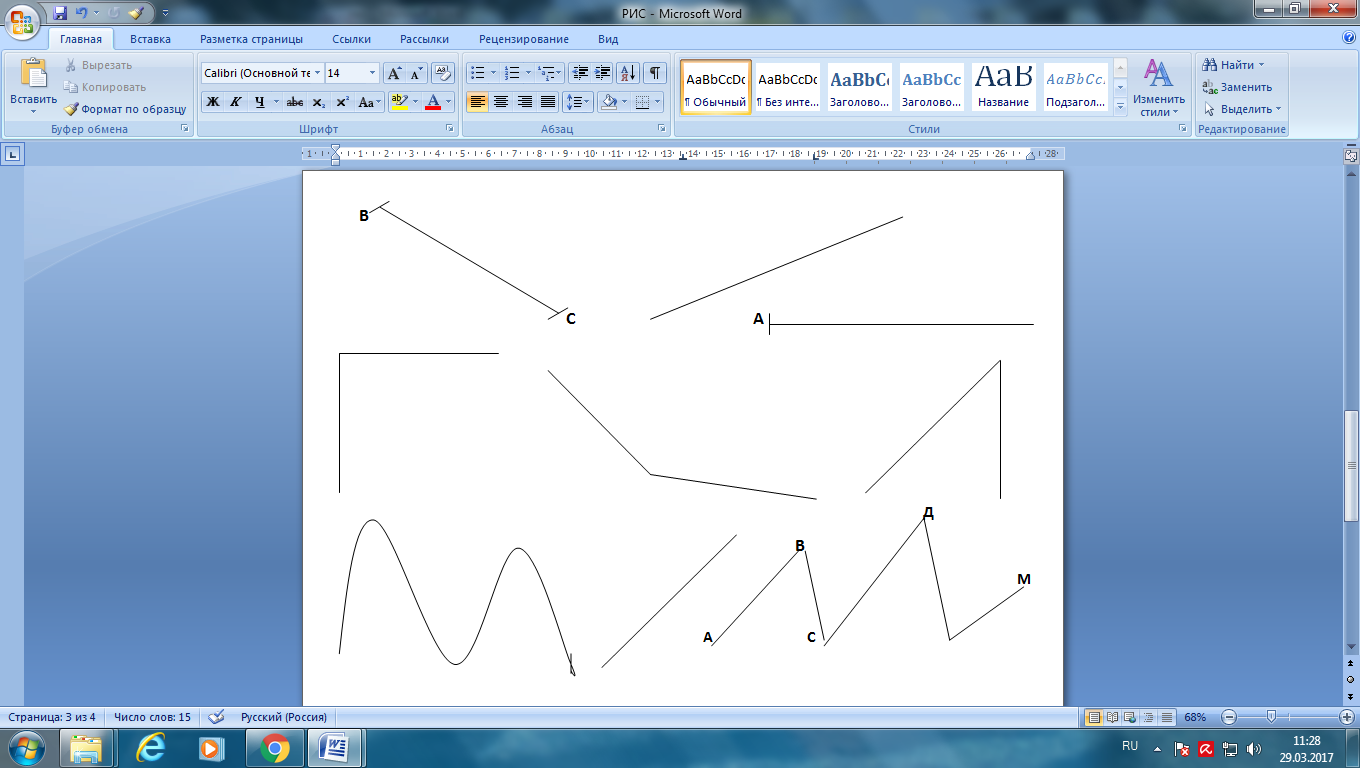
Отрезок Прямая линия Луч |
|
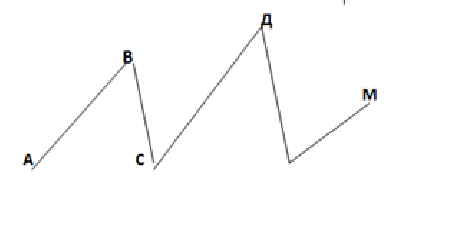
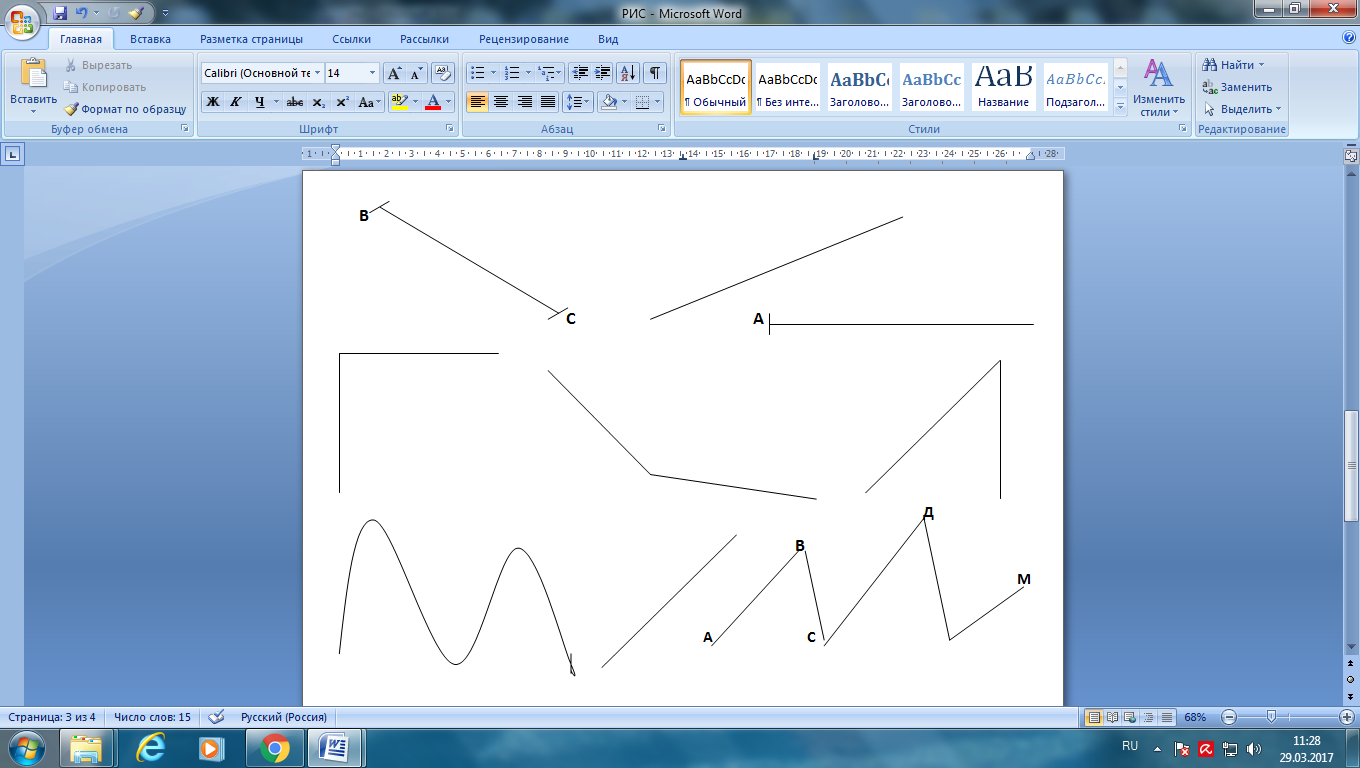
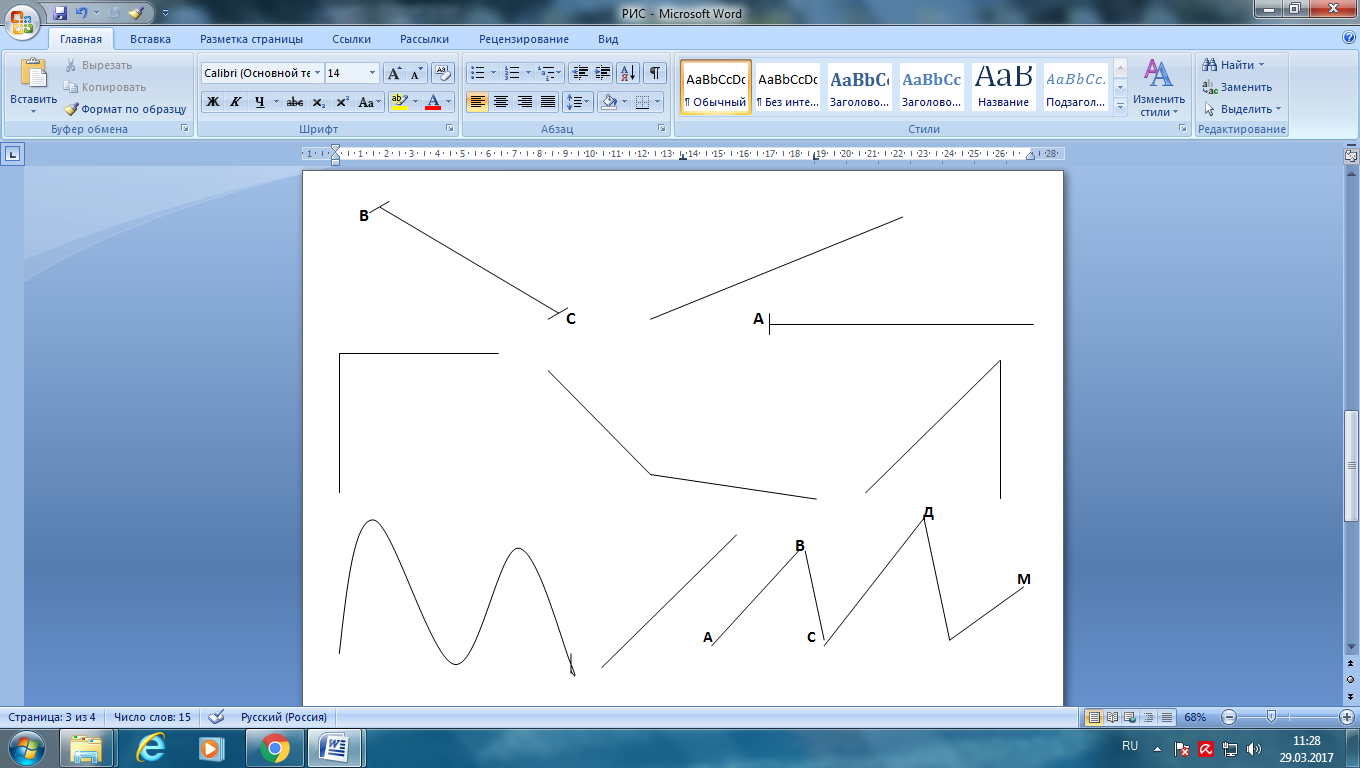
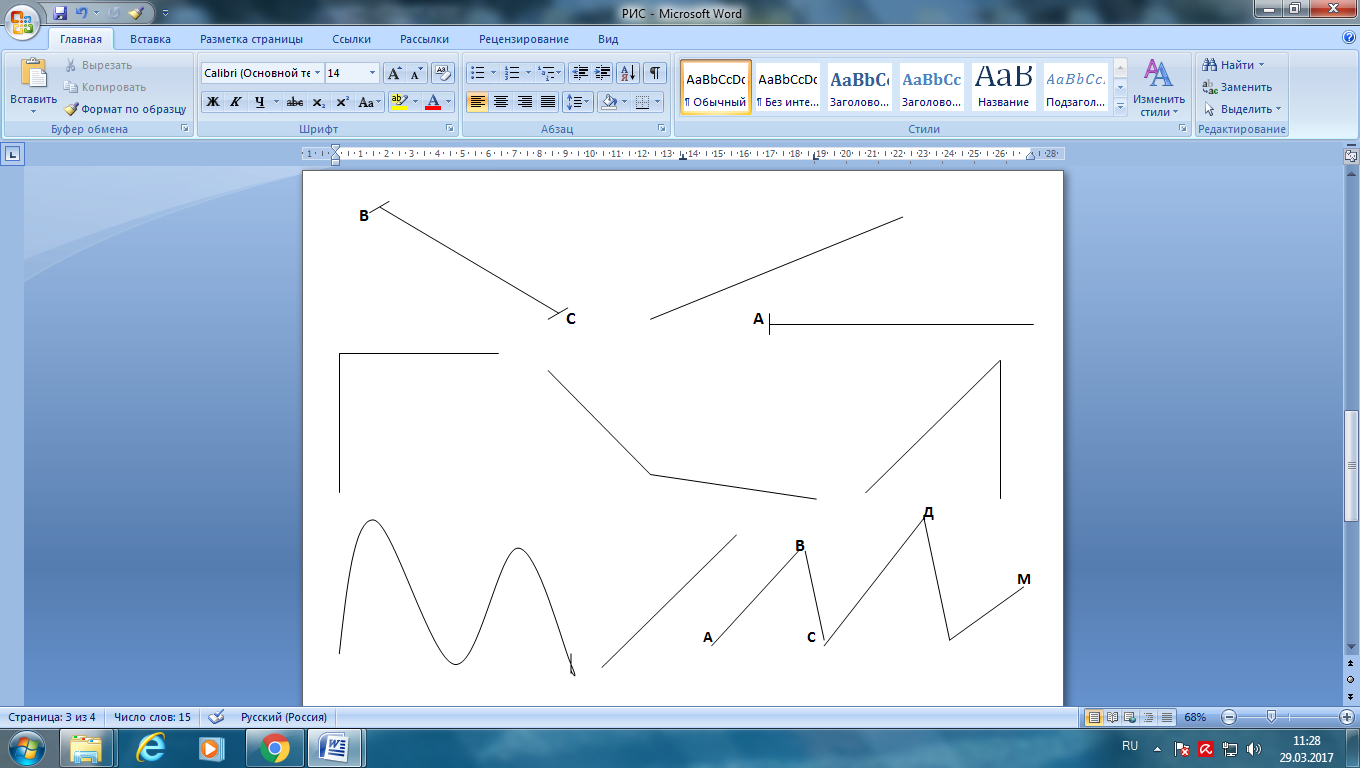
Кривая линия Прямая линия Ломаная линия |
|
Прямой угол Тупой угол Острый угол |
– Маршрут мы определили. Теперь построим ракету.
(На столах у детей разложены индивидуальные пакеты с различными геометрическими фигурами, из которых нужно построить ракету).
– Ракету мы построили. Для того, чтобы ракета взлетела, вам нужно ответить на некоторые вопросы:
1. Назовите геометрические фигуры, из которых построена ракета.
2. Какая фигура называется треугольником?
3. Назовите виды треугольников, различающихся по длинам сторон.
4. Назовите виды треугольников, различающихся по видам углов.
5. Назовите известные четырехугольники.
6. Какая фигура называется прямоугольником?
7. Какие стороны прямоугольника равны?
8. Какая фигура называется квадратом?
9. Какие углы у квадрата?
10. Что можно сказать о диагоналях квадрата?
11. Сколько диагоналей можно провести в прямоугольнике?
12. Можно ли всякий прямоугольник назвать квадратом? А всякий квадрат – прямоугольником?
13. Что мы называем радиусом круга?
14. Сколько можно провести радиусов в круге?
– Молодцы, вы хорошо справились с заданием. Можно лететь. Начинаю обратный отсчет: 5, 4, 3, 2, 1. Старт.
Геометрия удач.
У каждого из нас своя ПРЯМАЯ,
Им пересечься только раз дано.
И в их пересеченьи мы встречаем
Свою беду, судьбу, удачу, но
У каждого своя ОКРУЖНОСТЬ,
Непроводящий круг проблем, забот,
Потерянность, утраченность, ненужность
И новый к потепленью ПОВОРОТ.
У каждого из нас свой ТРЕУГОЛЬНИК.
И, убегая от страстей своих,
Мы мечемся, настигнутые болью
И счастьем, поделенным на троих.
А как нас век кидает и ломает!
Но на губах так мало добрых слов.
У каждого из нас своя КРИВАЯ
И ломанная с множеством УГЛОВ.
Дмитрий Челышев.
– Мы думали, что наше путешествие пройдет спокойно и без приключений. Но вот с Цветущей планеты поступил сигнал: “SOS”.
“На нашу планету напали пираты. Они похитили розу бессмертия”. Есть один способ спасти планету и вернуть розу, это решить три задачи. Жители планеты в ужасе, никто не может их решить. Если мы не поможем, планета погибнет.
Зачитывается текст телеграммы:
1. Начертить окружность с радиусом 3 см.
2. Начертить прямоугольник ABCD. Длина стороны AB равна 5 см, длина стороны BC равна 2 см. Провести диагональ.
3. Начертить ломаную линию KMNOS: KM = 2 см, MN = 5 см, NO = 6 см, OS = 3 см. Найти длину ломаной.
Дети выполняют задание в тетради. Для выполнения заданий на доске вызвать трех учеников.
– Молодцы, вы хорошо справились с заданием. Мы вернули розу бессмертия на Цветущую планету. В благодарность жители планеты подарили нам стихотворение.
Геометрия трав.
Математик несбывшийся, странник,
Оглядись, озираясь стократ:
В травах срез волчеца – ПЯТИГРАННИК,
А сеченье душицы – КВАДРАТ.
Всё на свете покажется внове
Под гольцом, чья ВЕРШИНА в снегу:
Водосбор – ТРЕУГОЛЕН в основе
На цветущем альпийском лугу!
Где ж, он КРУГ?
Возле иглистой розы,
там, где луг поднебесный скалист,
вижу – с ветром играет березы
ТРЕУГОЛЬНО-РОМБИЧЕСКИЙ лист…
Равиль Бухарев.
– Мы подлетели к Белой планете. Планета условно обозначена в форме круга, треугольника и квадрата. По просьбе жителей планеты нам нужно запустить экспериментальные ракеты с краской и разукрасить планету.
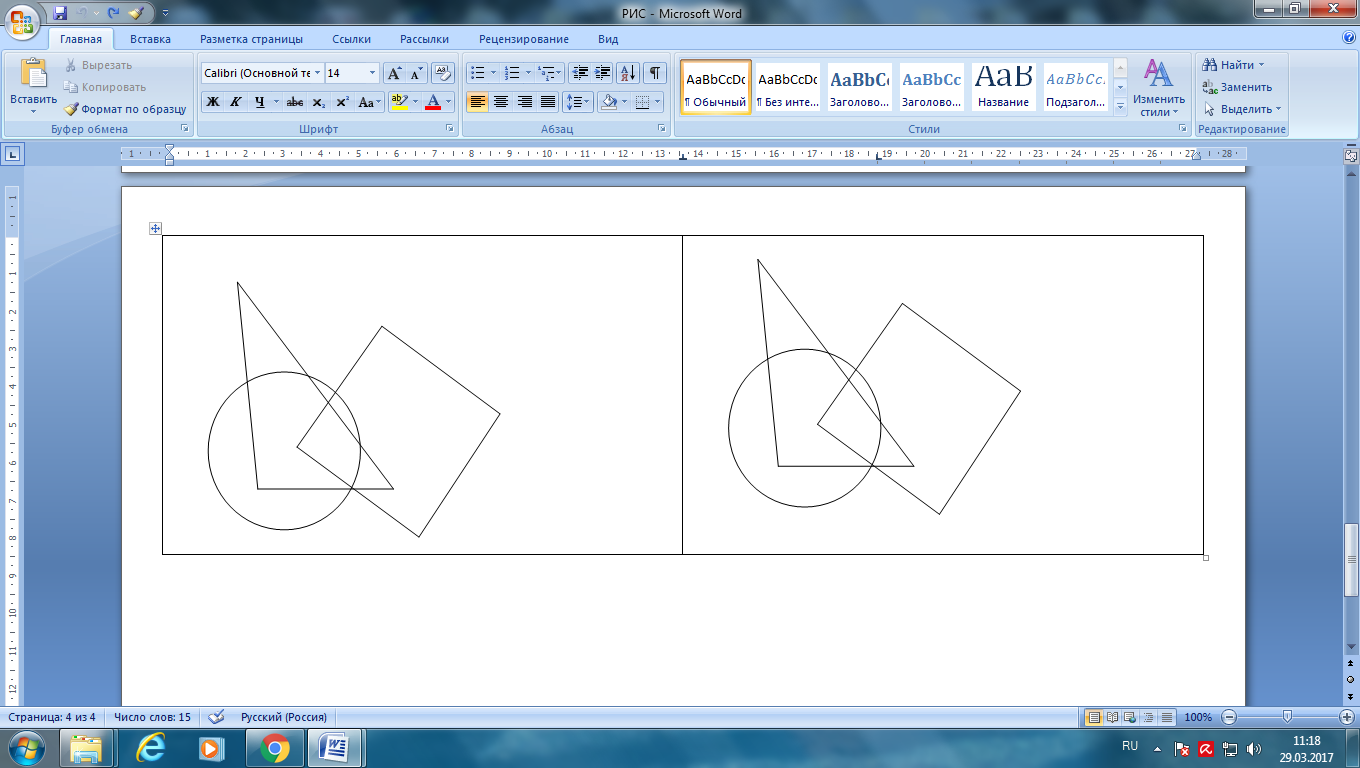
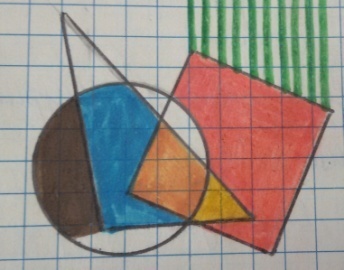
(На столах у детей индивидуальные карточки с рисунком планеты.
По одному ученику выходят к доске и раскрашивают рисунок планеты на плакате).
– Итак, даю команды: “Приготовьте цветные ракеты – карандаши. Начали!”
Первый запуск – красную ракету направляем в точку, которая находится в квадрате, но за кругом и треугольником.
Второй запуск – желтую ракету направляем в точку, которая находится в треугольнике и квадрате, но за кругом.
Третий запуск – зеленую ракету направляем в точку, которая находится над квадратом и справа от круга.
Четвертый запуск – синюю ракету направляем в точку, которая находится в треугольнике и круге, но за квадратом.
Пятый запуск – коричневую ракету направляем в точку, которая находится в круге и слева от треугольника.
Шестой запуск – оранжевую ракету направляем в точку, куда обязательно входят части всех фигур (круга, квадрата, треугольника).
– Все выполнили? Отложите карандаши. Молодцы!
Летим дальше.
Треугольник и квадрат.
Жили-были два брата –
Треугольник с Квадратом.
Старший – квадратный,
Добродушный, приятный.
Младший – треугольный,
Вечно недовольный.
Стал расспрашивать Квадрат:
– Отчего ты злишься, брат?
Тот кричит ему:
– Смотри!
Ты полней меня и шире.
У меня углов лишь три,
У тебя же их четыре.
Но Квадрат ответил:
– Брат!
Я же старше, я – Квадрат.
И сказал ещё нежней:
– Неизвестно, кто нужней!
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя, сказал:
– Приятных я тебе желаю снов!
Спать ложился ты квадратным,
А проснёшься без углов.
Но наутро младший брат,
Страшной мести был не рад.
Поглядел он – нет Квадрата.
Онемел… Стоял без слов…
Вот так месть! Теперь у брата
Восемь новеньких углов!
Л.В. Литцман
– На горизонте показалась Планета головоломок. Жители планеты приготовили нам загадку.
Даны три ряда изображений самолетов, отличающихся формой корпуса, крыльев, их окраской, количеством иллюминаторов. Недостающий самолет надо выбрать из шести фигур, помещенных справа. Ответ обосновать, указывая признаки той фигуры, которая должна быть помещена в пустой квадрат.
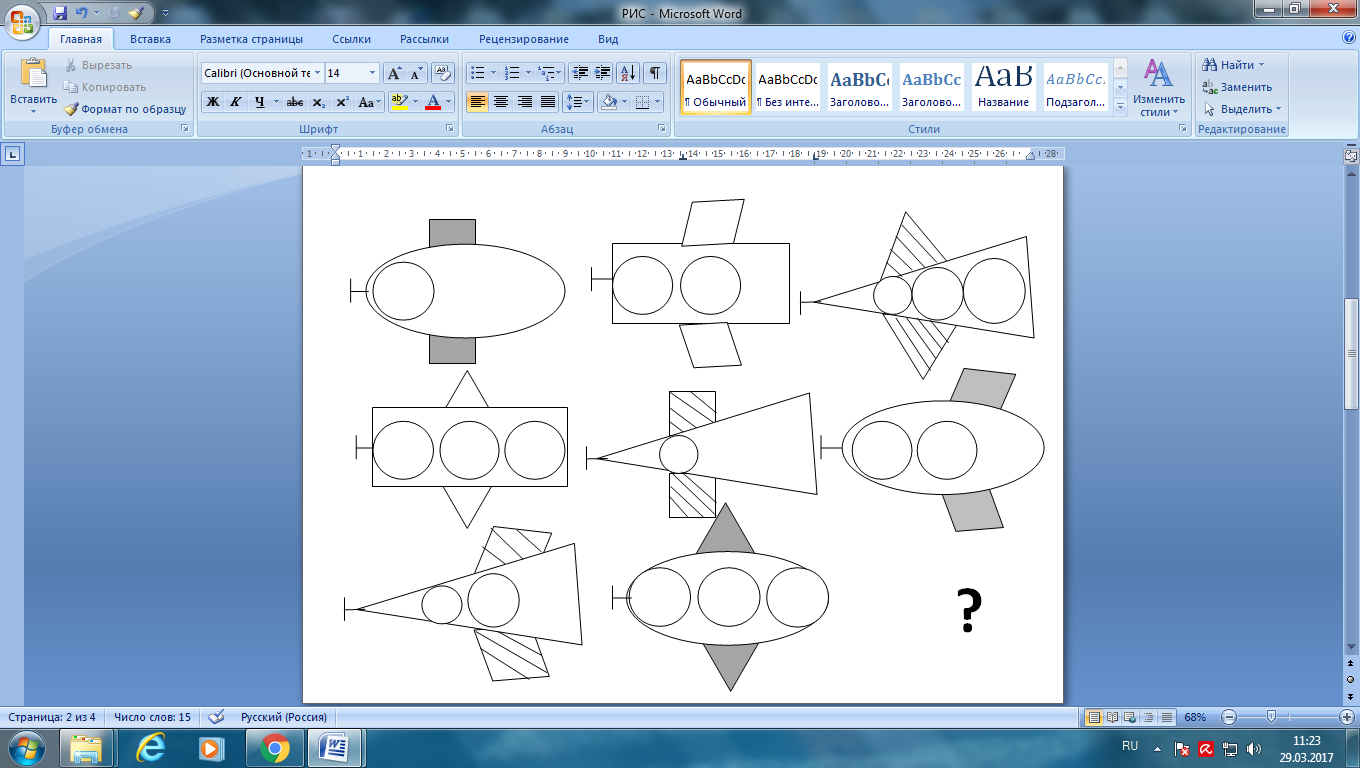
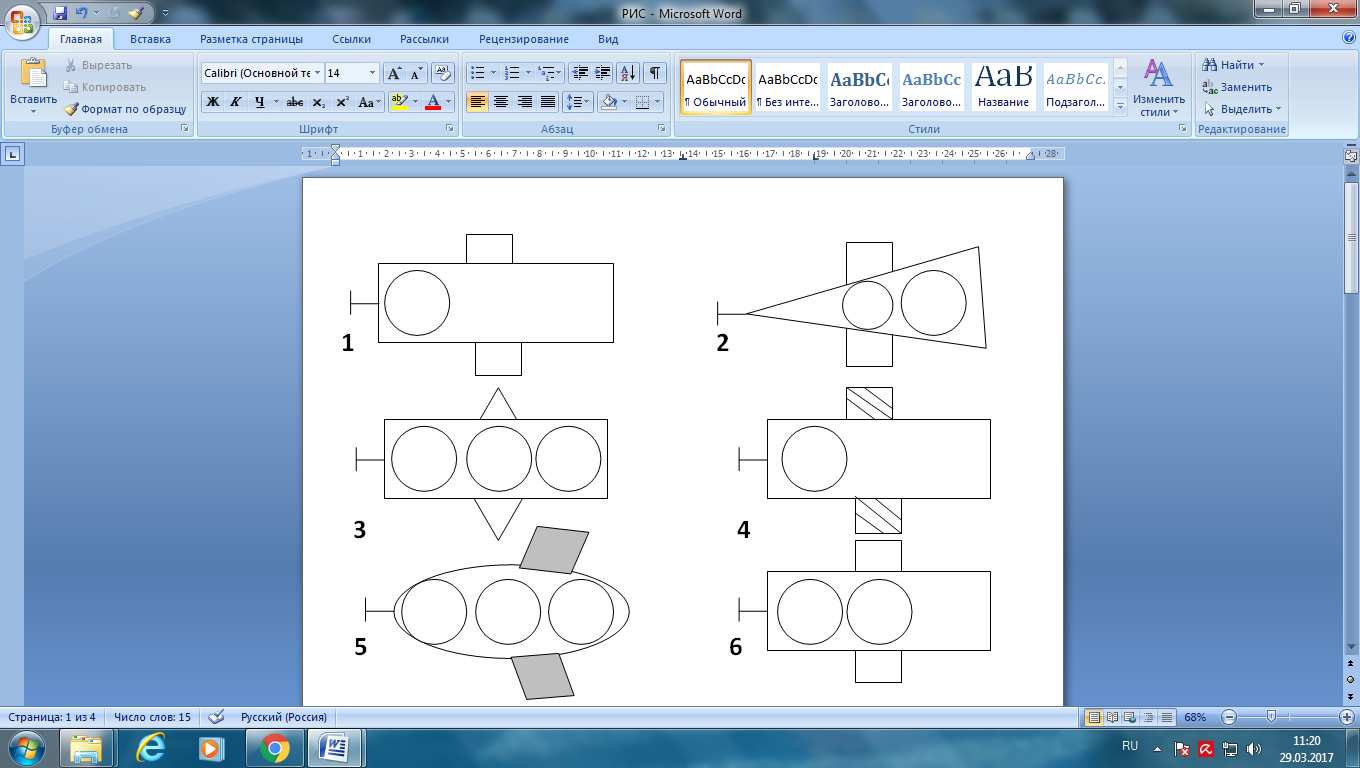
– Вы хорошо справились с заданием.
Завершилось наше путешествие и пора возвращаться на Землю. За время полета мы многое повторили, узнали что-то новое. Все очень хорошо поработали. Молодцы!
III. Итоги урока. Выставление оценок.
IV. Домашнее задание: составить ковер из геометрических фигур.