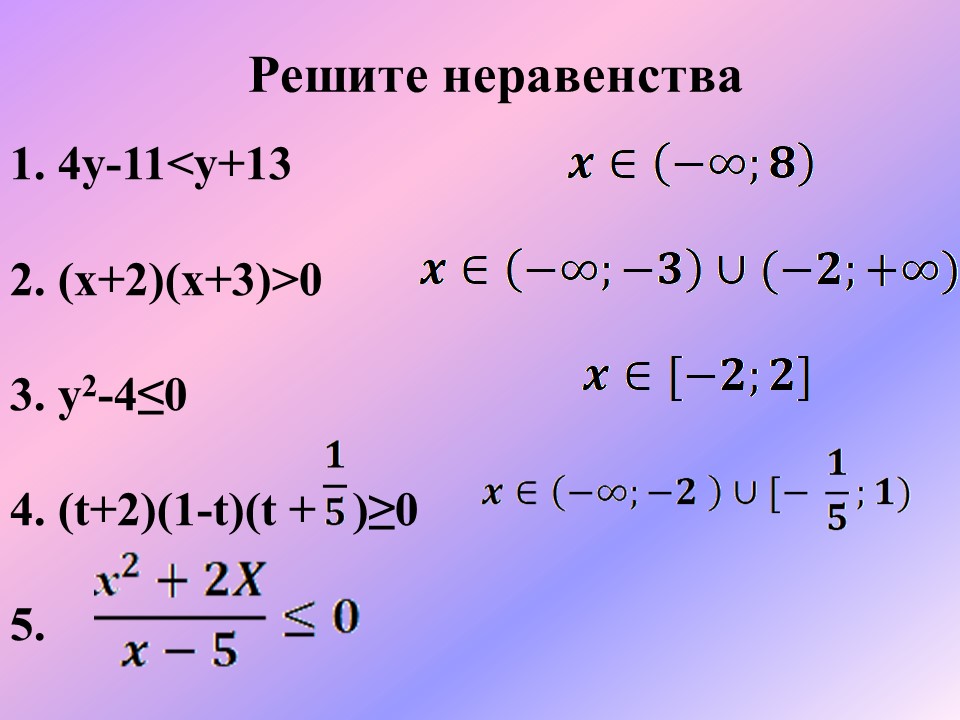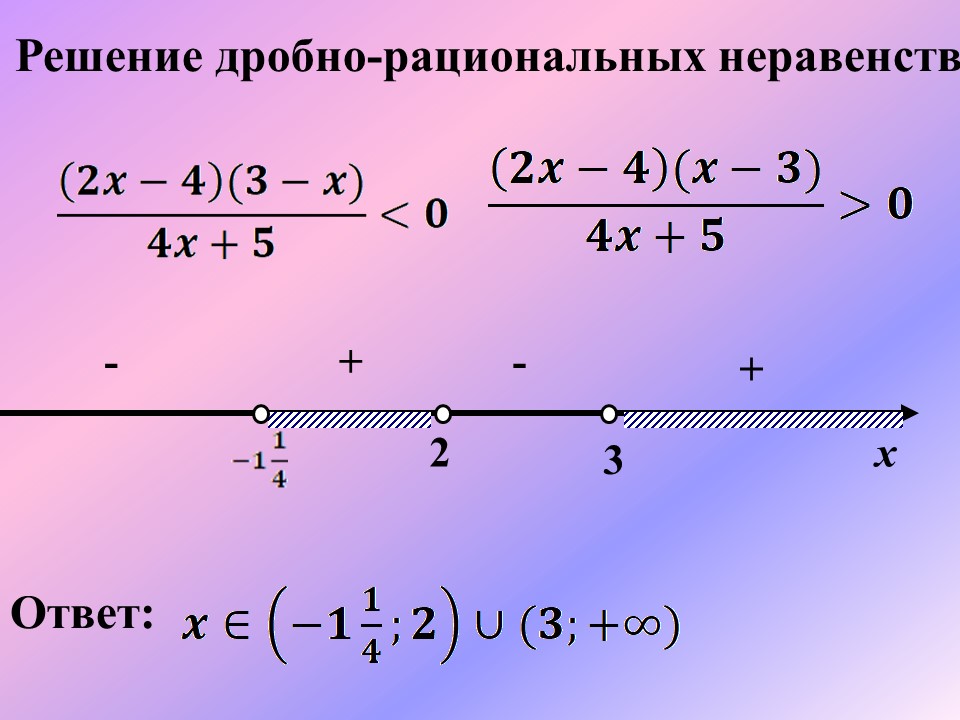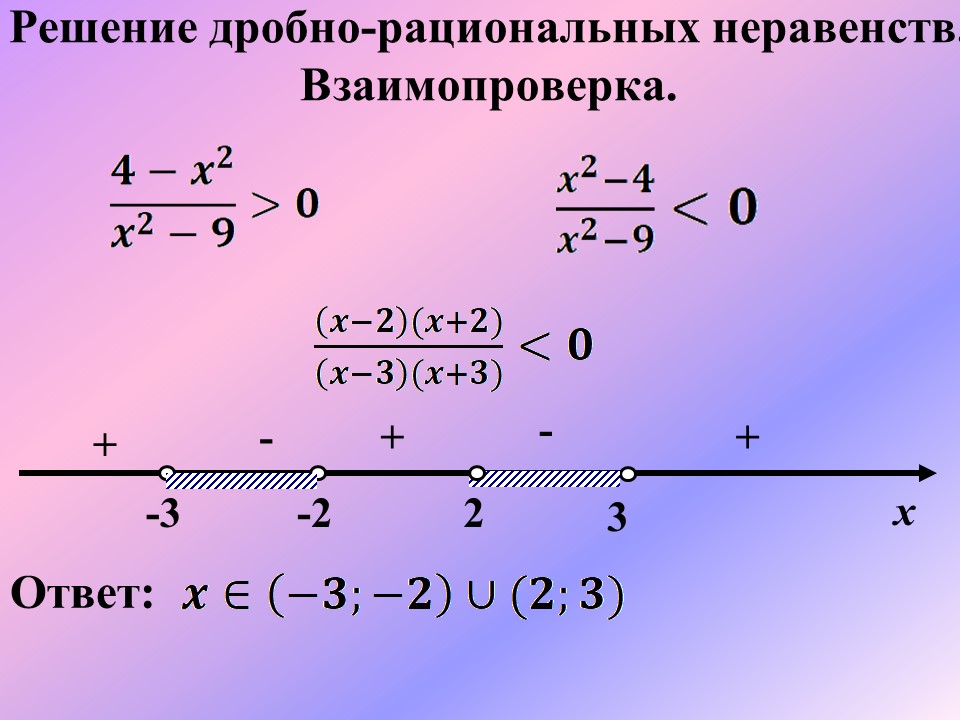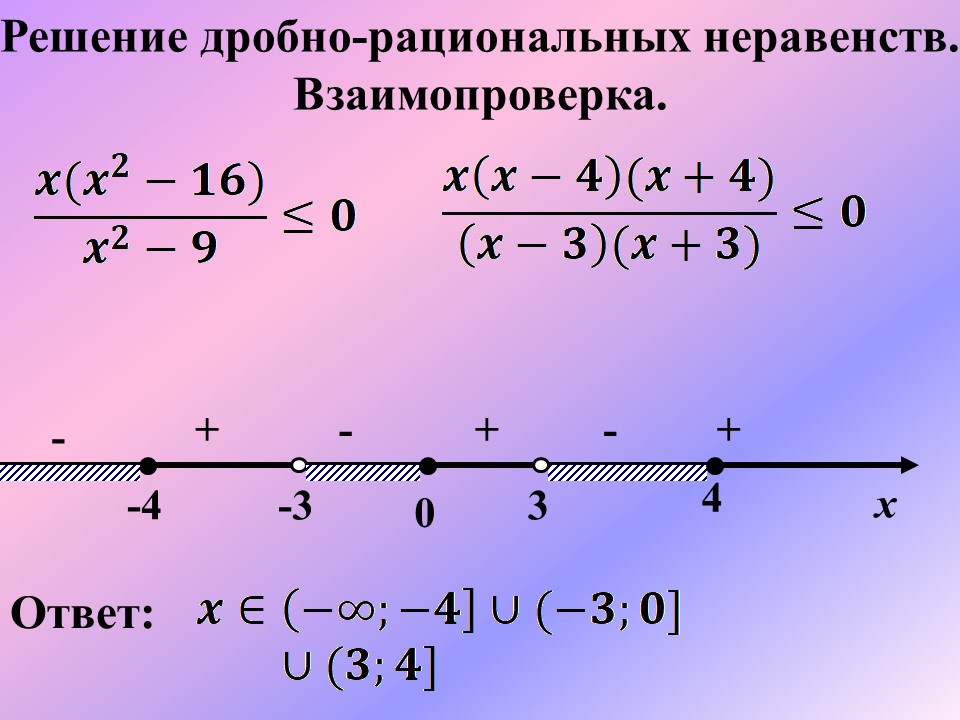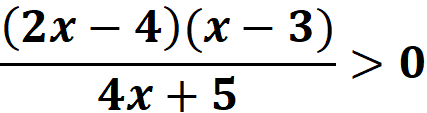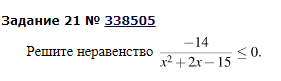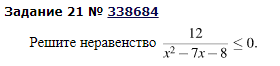Дробно-рациональные неравенства

Предмет

Алгебра

Класс

9

Тип урока

Урок изучения нового.

Авторы УМК

Алгебра. 9 класс. В 2ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича. – 11-е изд., стер. – М.: Мнемозина, 2009. – 223 с. Алгебра. 9 класс. В 2ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П.В. Семенов. – 11-е изд., стер. – М.: Мнемозина, 2009. – 224 с.

Продолжительность урока:

45 минут.

Цель:

создать условия для осознания и осмысления блока новой учебной информации, научить решать учащихся рациональные неравенства.

Планируемые образовательные результаты (личностные, метапредметные, предметные):

Личностные: умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, оценивать себя и своих товарищей, формирование уважительного отношения к иному мнению.

Метапредметные: способность самостоятельно преобразовывать практическую задачу в познавательную; умение планировать собственную деятельность в соответствии с поставленной задачей и условиями ее реализации и искать средства ее осуществления; умение контролировать и оценивать свои действия, развитие мыслительных операций посредством сравнений, сопоставлений, обобщений; развитие потребности к самообразованию.

Предметные: понимание учащимися, что значит решить рациональное неравенство, дробно-рациональное неравенство; усвоение алгоритма решения рациональных неравенств.

Оборудование:

Классная доска, учебник, интерактивная доска.

1

Этап мотивации к коррекционной деятельности

Приветствует класс, проверяет готовность к уроку.

Подготовка класса к работе. Называют отсутствующих.

Коммуникативные:

-планирование учебного сотрудничества со сверстниками

Личностные

-готовность учащихся к уроку

Познавательные

-самостоятельное выделение и формулирование поставленной цели.

-психологическая готовность

2

Этап «Актуализации знаний и пробного учебного действия».

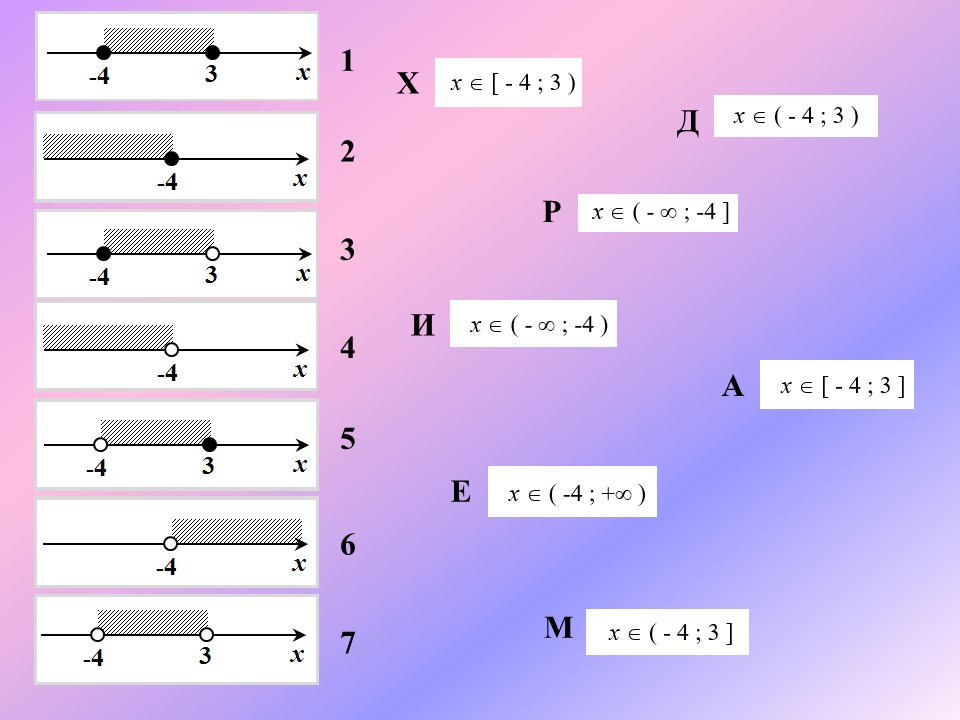
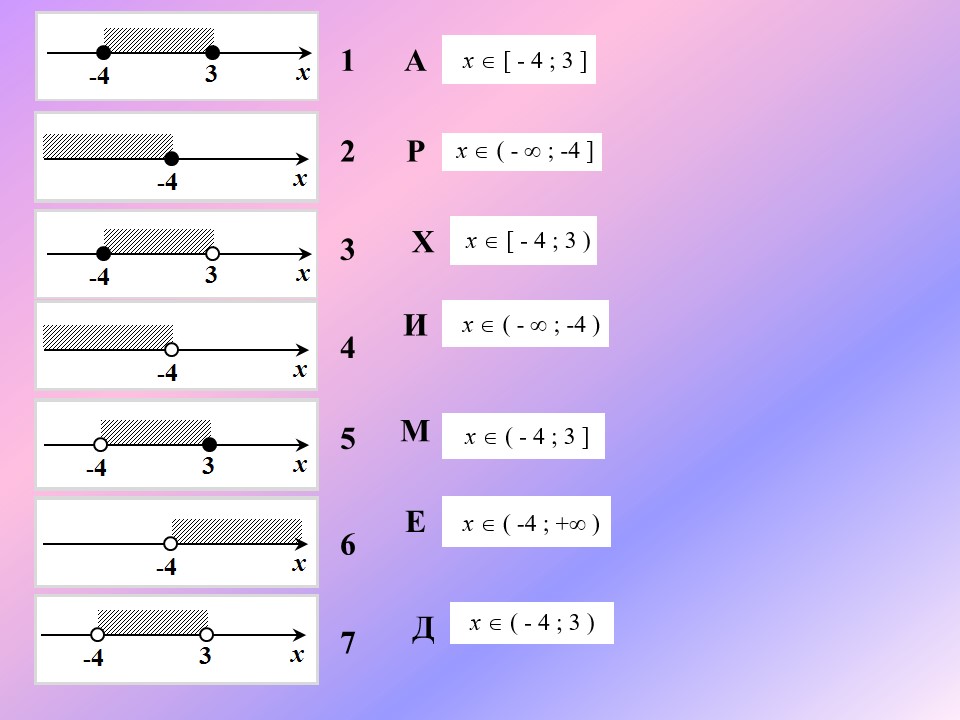
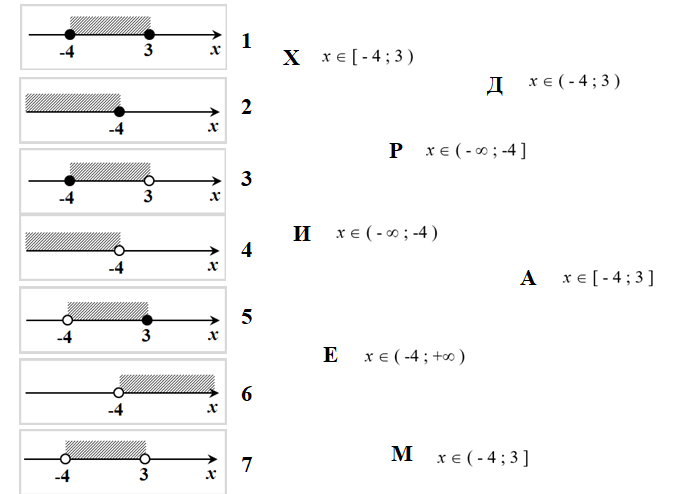
(Активизирует деятельность учащихся.)

1. Понятиями неравенства пользовались уже древние греки. Великий математик в (III в. до н. э.), занимаясь вычислением длины окружности, установил, что «периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых». Иначе говоря, Он указал границы числа Пи.

А кто это был, вы сейчас узнаете из решения следующей задачи. Вам нужно соотнести правильно числовые промежутки и геометрическую модель решения неравенства. И сопоставить числа и буквы.

Проверка:

Для тех, кто не справился с данной задачей, предлагаю на вооружение мордашки – строгую и не строгую!

Определяют числовые промежутки, находят имя известного математика.

Корректируют свои знания в случае ошибочных ответов.

Личностные

-развитие внимания, памяти. Предметные:

-применение теоретических и практических знаний по теме.

Регулятивные :

-планирование своей деятельности для решения поставленной задачи,

-контроль полученного результата,

Коррекция полученного результата.

3

Постановка учебной задачи

(Создает проблемную ситуацию, организует учащихся по исследованию проблемной ситуации)

Следующим этапом вашей работы будет решение известных вам неравенств:

1. 4y-11<y+13; Ответ:

2. x²+5x+6>0 Ответ:

3. y²-4≤ 0 Ответ:

4. (t+2)(1-t)(t +)≥0 Ответ:

5.

У доски разбираются задания 1-4, акцентируется внимание на решение рациональных неравенств методом интервалов.

– Виды каких неравенств вы знаете?

– С каким неравенством возникли трудности? Почему?

– Что вы можете сказать о пятом неравенстве, чем оно отличается от других? (это дробь)

– Как вы думаете, как будет звучать тема нашего урока?

-Какие цели можно перед собой поставить?

Учащиеся работают в парах, обсуждая задание. Комментируют полученный результат, устно отвечают на вопросы по слайду. Выявляют проблему, ставят цель, формулируют и записывают тему урока.

(Дробно-рациональные неравенства)

Коммуникативные:

-управление поведением партнера-контроль, оценка действий партнера,

-умения работать в группах, развитие диалогической речи

Регулятивные :

-планирование своей деятельности для решения поставленной задачи,

-контроль полученного результата,

Коррекция полученного результата.

4.

Процессуально-познавательный этап (Изучение нового материала, закрепление изученного материала)

Рациональное неравенство представляет из себя такое неравенство с переменными, которое содержит в обеих частях рациональные выражения.

Целое рациональное неравенство состоит из целых рациональных выражений (в обеих частях).

Дробно рациональное неравенство – это такое неравенство, которое содержит дробное выражение в одной или обеих своих частях.

Давайте вместе решим данное неравенство вместе:

Для решения любого рационального неравенства, нужно преобразовать его, разложив на множители числитель и знаменатель.

Преобразуем и получаем:

При каких значениях x, данное неравенство будет равно нулю, какое условие мы должны включить в решение данного неравенства? (Знаменатель не равен нулю).

То есть на числовой прямой мы отмечаем три точки, две из которых закрашены, то есть принадлежат промежутку, а другая – пустая. Какие значения у этих точек?

Ответ:

Скажите, при решении дробно-рациональных неравенств, применимы ли ранее изученные правила решения неравенств?

Предлагаю решить данное неравенство совместно у доски , (вызывает к доске ученика, желающего решить данное неравенство).

Ответ:

Следующий этап для усвоения нового материала-

работа в парах со взаимопроверкой.

№ 2.16(а,б)

Решить неравенства. (Каждый ученик решает по два неравенства со взаимовпроверкой)

а)

б)

№ 2.26

а)

б)

ВЗАИМОПРОВЕРКА

№2.16 (а,б)

№ 2.26

а) ; ;

Ответ:

б) ;

; ;

Ответ:

Решают рациональное неравенство вместе с учителем, анализируют, задают вопросы в случае затруднения понимания новой темы.

Решают совместно неравенство с одноклассниками у доски.

Закрепление и коррекция нового материала.

Работа в парах,

Проверка решенных неравенств у доски, коррекция заданий, решенных не правильно.

Коммуникативные:

– развитие диалогической речи

Регулятивные:

-планирование своей деятельности для решения поставленной задачи,

-контроль полученного результата,

-коррекция полученного результата

5.

Этап самостоятельной работы с самопроверкой

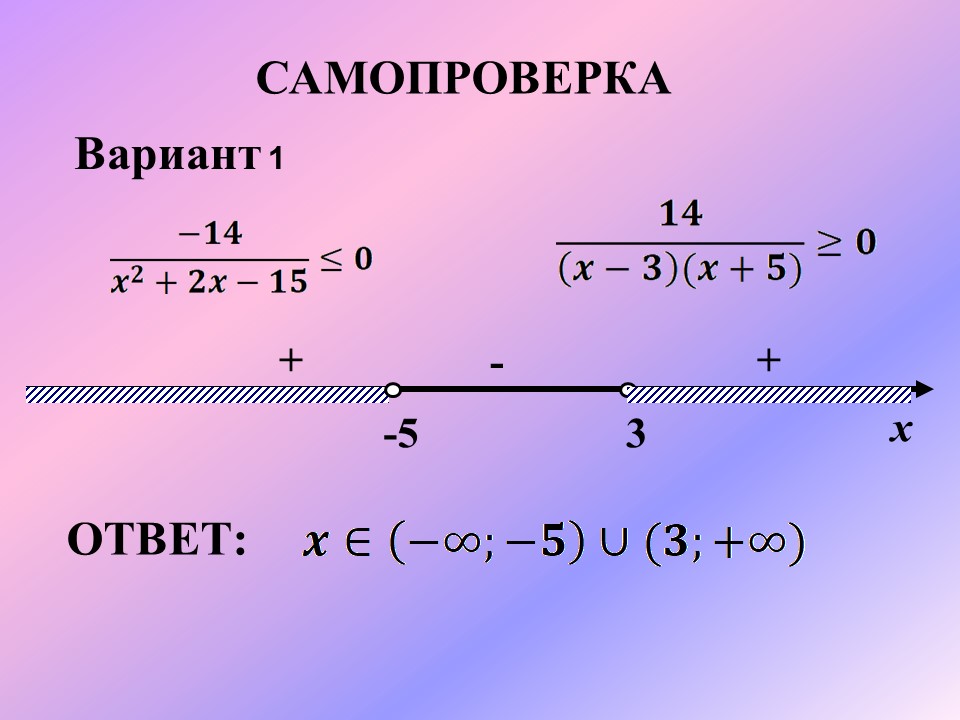
Для закрепления нового материала предлагает выполнить учащимся аналогичные неравенства, которые взяты из банка заданий сайта СДАМ ГИА под номером 21 ОГЭ по математике

на отдельных листочках, после решения сдают учителю.

Вариант 1

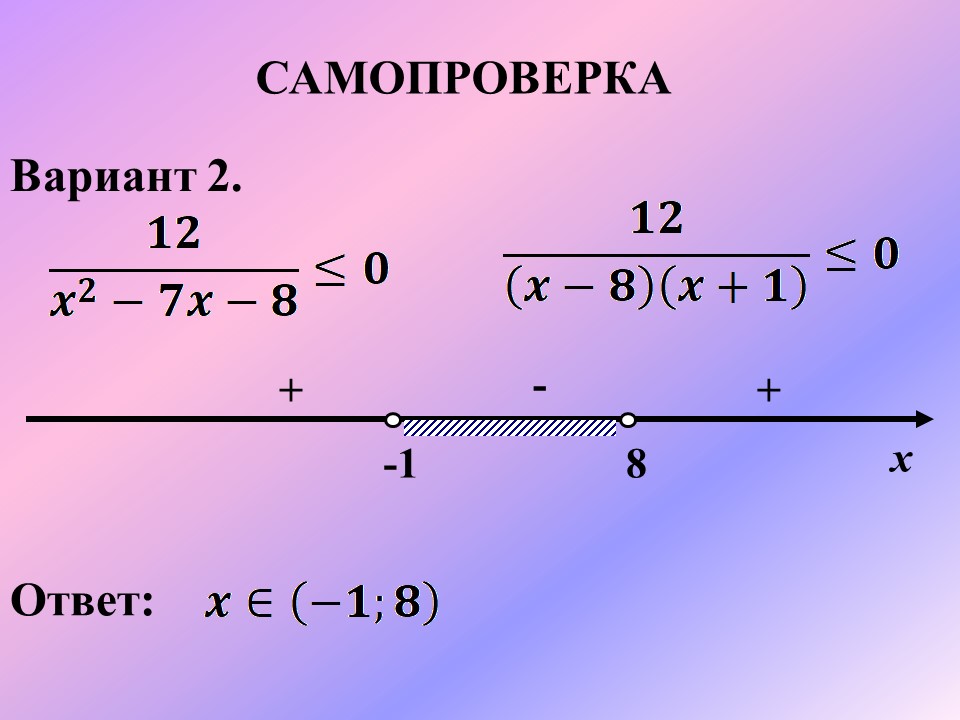
Вариант 2.

Самопроверка.

Так как разложение многочлена на множители у нас только в знаменателе, а знаменатель не равен нулю, то точки на числовой прямой у нас будут пустыми.

Вариант 1

;

Вариант 2.

;

Самостоятельно решают рациональные неравенства, корректируют приобретенные знания.

Познавательные

-умение структурировать знания,

– выбор наиболее эффективных способов решения поставленной задачи

6.

Этап рефлексии деятельности на уроке

(Подведение итогов урока,

информация о домашней работе.)

Подходит к завершению наш урок, пора подвести итоги.

Какие виды неравенств вами были изучены? Каким методом мы решаем рациональные неравенства?

О чем мы сегодня говорили? Какие неравенства называются дробно-рациональными?

Домашняя работа – Домашняя работа, сформированная в учебной платформе Якласс.

Рефлексия учебной деятельности

• было интересно…
• было трудно…
• я понял, что…
• я научился…
• у меня получилось …
• урок дал мне для жизни…

Учащиеся отвечают на вопросы учителя.

Регулятивные:

-осознание качества и уровня усвоения знаний

Личностные

-адекватное понимание причин успеха/не успеха в учебной деятельности

Познавательные

-анализ деятельности,

-установление причинно-следственных связей.